
alhimar worksheets tutors

circle radius equation center
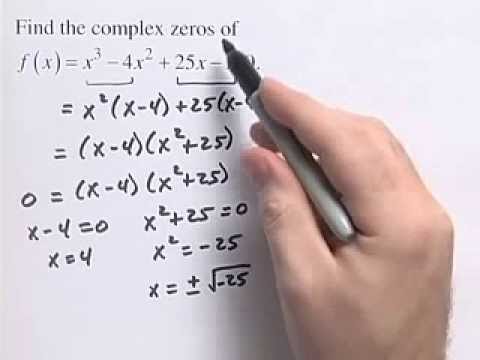
zeros complex polynomial function finding algebra
This section shows how to find general and particular solutions of simple differential equations. From the above examples, we can see that solving a DE means finding an equation with no derivatives that satisfies the given DE.
The complete solution to such an equation can be found by combining two types of solution On Introduction to Second Order Differential Equations we learn how to find the general solution. Which is a quadratic equation that has three possible solution types depending on the
Systems of linear equations and their solution, explained with pictures , examples and a cool interactive applet. Also, a look at the using substitution, graphing and elimination Ok, so what is the solution of a system of equations? Answer. The solution is where the equations 'meet' or intersect.
In this video, I show how to find the real solutions of an equation by using a TI-83 plus graphing calculator. The procedure applies to all equations
Solve quadratic equation by factoring or using quadratic formula with our free quadratic equation calculator. The standard form of a quadratic equation is ax2 + bx + c = 0 when a ≠ 0 and a, b, and c are real numbers. Step 2 Factor completely. Recall how to factor trinomials.
Solution: To check whether the equation has a solution or not, quadratic formula for discriminant is used. Find number of solutions of a linear equation of n variables.
How Many Solutions Can an Equation Have? Okay, algebristas,* different equations can have different numbers of solutions. Right now, we're only counting solutions from the real numbers. Some equations have solutions that are imaginary numbers, but we'll get to those later. No, you don't
Finding a linear equation is very straightforward if the slope and y-intercept are given. This is certainly not always the case; however, the example demonstrates that the algebraic equation of a line depends on these It is useful for finding the equation of a line given the slope and any ordered pair solution.
Today, we will find the real solutions of an equation. In this video, I show how to find the real solutions of an equation by using a TI-83 plus graphing calculator. The procedure applies ...
How to know which interval includes the real solutions to this? Related Threads on Find real solutions to an equation. Can you help me to find the solution of logarithm equation.
See how some equations have one solution, others have no solutions, and still others have infinite solutions. So we're in this scenario right over here. We very explicitly were able to find an x, x equals 1/9, that satisfies this equation.
In a cubic equation, the highest exponent is 3, the equation has 3 solutions/roots, and the equation itself takes the form ax^3+bx^2+cx+d=0. While cubics How to Solve a Cubic Equation. Download Article. 1 Solving Cubic Equations without a Constant. 2 Finding Integer Solutions with Factor Lists.
Differential Equations Solutions: A solution of a differential equation is a relation between the A General Solution of an nth order differential equation is one that involves n necessary arbitrary Also find the particular solution of the given differential equation satisfying the initial value conditions f(0)...
Procedure for finding general solution of linear second-order difference equation with constant coefficients. We can use the earlier result characterizing the solutions of the homogeneous equation to find conditions under which these solutions converge to zero, as follows.
Set the factors equal to zero. find the real solution for each equation? find the remaining zeros of the polynomial?
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Equation Calculator. Solve linear, quadratic, biquadratic. absolute and radical equations, step-by-step.
Essential Question: How can you find the complex solutions of any quadratic equation? Resource Locker. Common Core Math Standards. Example 2 Answer the question by writing an equation and determining whether the solutions of the equation are real or non-real.
$\begingroup$ @MichaelE2 The question asks how we should find all real solutions of the equation but the post incorectly says that there is only Analogous details one can find checking the Reduce page. When we don't specify the domain, then by default it is assumed to be Complexes but as

polynomial functions function graph graphs sketch section equation zero determine quadratics math then behavior end number 6x 5x
Free Online Equation Calculator helps you to solve linear, quadratic and polynomial systems of equations. Answers, graphs, alternate forms. Wolfram|Alpha is a great tool for finding polynomial roots and solving systems of equations. It also factors polynomials, plots polynomial solution

differential mixing equations order applications
...solutions and equations with both real and imaginary solutions the same way: find the solutions, and discard the ones that are not real numbers. Simplify the equation as much as possible. For instance, if given the equation x4 + x2 - 6 = 0, you can use a u-substitution to simplify and then factor.
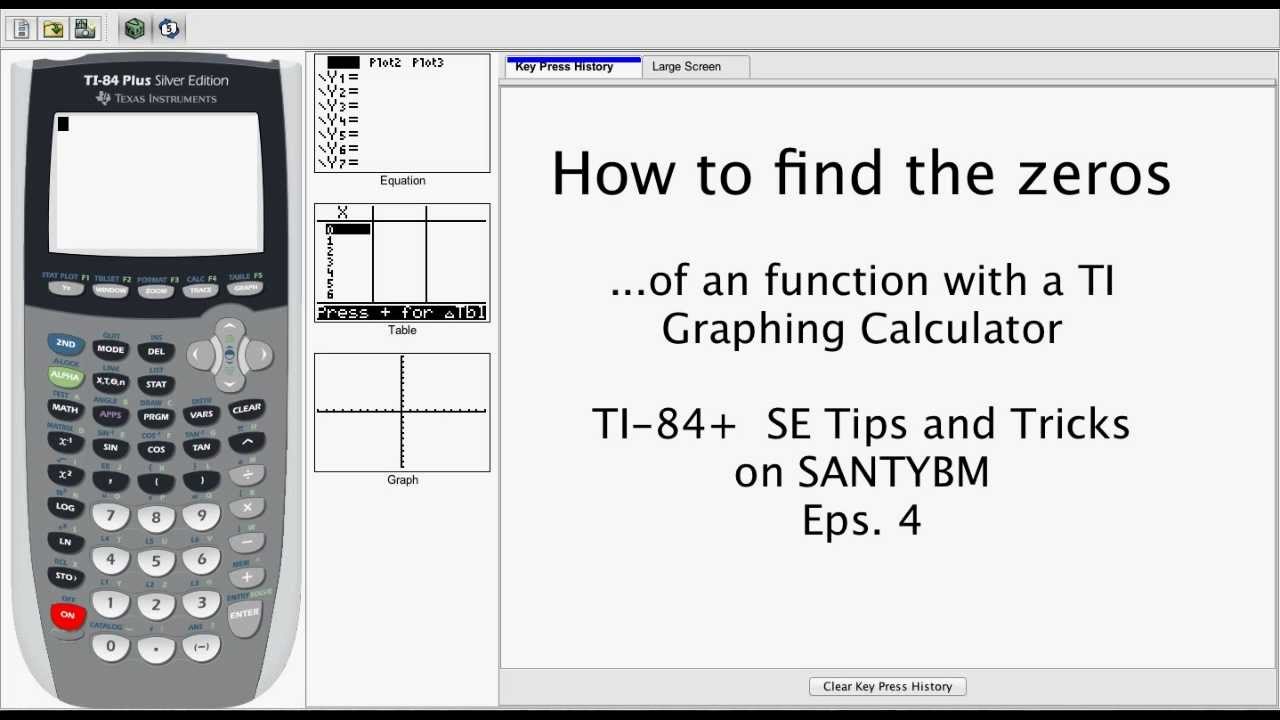
calculator graphing using finding zeros ti 84 graph ti84 equation plus equations value table solve sets absolute se graphs
In mathematics, to solve an equation is to find its solutions, which are the values (numbers, functions, sets, etc.) that fulfill the condition stated by the equation, consisting generally of two expressions related by an equals sign.
We will also show how to sketch phase portraits associated with real distinct eigenvalues must be nonsingular and hence these two solutions will be a fundamental set of solutions. we can see that the solution to the original differential equation is just the top row of the solution to the matrix system.
Linear equations involve unknown quantities in the form of one or more variables to represent real-life problems. It helps in finding out the cost, mileage, speed, and distance In this lesson, let us learn in detail about the solutions of linear equations, types of solutions, and how to find the solutions, etc.
A quadratic equation has no solution when the discriminant is negative. Given a pair of complex conjugate solutions, we want to find a quadratic equation that has those This article goes into detail on how to use a quadratic to find the nature of the solutions (real or complex) of a cubic function.
Now we will see how to solve a radical equation. Sometimes after squaring both sides of an equation, we still have a variable inside a radical. We used the formula to find the area of a rectangle with length L and width W. A square is a rectangle in which the length and width are equal.
Now the question rises here that how to find the real solution of a cubic equation, so, let's start. First we consider, And then we will find the discriminant as given by. If then there are repeated roots as follows.

quadratic discriminant equations linear equation using solving ppt graphing utility solution solutions powerpoint presentation unequal slideserve
how to obtain solutions of quadratic functions graphically, how the solutions of a quadratic equation is related to the graph of the quadratic function, how to The following diagrams show the three types of solutions that a quadratic equation can have: two solutions, one solution and no real solution.

solutions number determine quadratic equations using discriminants
Therefore, finding the root of a function implies finding the value of such that the function is zero. The software will be all the more useful in this case since solving this type of algebraic equations is often impossible. For example, there are no solution methods that will find the value of such that
Calculator solution will show work for real and complex roots. Uses the quadratic formula to solve a second-order polynomial equation or quadratic equation. Shows work by example of the entered equation to find the real or complex root solutions.

quadratic solving equations graphically using intercepts
. So, we had a real equation and we found real roots. The thing is that to do so we needed to take a detour through complex-land, which is actually A reasonable result would be that you want it to be a unique solution of an equation (or perhaps finite system of equations) that we can write down:
