How. Details: Find the eigenvectors and eigenvalues of the following matrix: Solution: To find eigenvectors we must solve the equation below for each eigenvalue: The eigenvalues are the roots of the characteristic equation: The solutions of the equation above are eigenvalues and they are equal

Find the matrix in reduced row echelon form that is row equivalent to the given m x n matrix A. Specify matrix dimensions. Please select the size of the matrix from the popup menus, then click on the "Submit" button. Number of rows: m =.

Examples of How to Find the Determinant of a 3×3 Matrix. The set-up below will help you find the correspondence between the generic elements of the formula and the elements of the actual problem.

Collectives on Stack Overflow. Find centralized, trusted content and collaborate around the technologies you use most. I'm trying to calculate eigenvalues and eigenvectors of a 3x3 hermitian matrix (named coh). Here is the matlab code I'm using

Matrices for which the eigenvalues and right eigenvectors will be computed. Finally, it is emphasized that v consists of the right (as in right-hand side) eigenvectors of a. A vector y satisfying @ a = z * for some number z is called a left eigenvector of a, and, in general, the left

Finding of eigenvalues and eigenvectors. This calculator allows to find eigenvalues and eigenvectors using the Characteristic polynomial. Matrix exponential. Display decimals , number of fraction digits: number of significant digits

Free matrix calculator - solve matrix operations and functions step-by-step. \mathrm{unit}. See All area asymptotes critical points derivative domain eigenvalues eigenvectors expand extreme points factor implicit derivative inflection points intercepts inverse laplace inverse laplace partial

Sal shows how to find the inverse of a 3x3 matrix using its determinant. In Part 1 we learn how to find the matrix of minors of a 3x3 matrix and its cofactor matrix.

matrix unit 3x3 eigenvalues eigenvectors corresponding

2 Finding the matrix of a transformation. Eigenbasis and diagonal matrix. 3 Examples in 2 dimensions. Stretching. Squeezing. . The resulting equation is known as eigenvalue equation.[5] The eigenvectors and eigenvalues are derived from it via the characteristic polynomial.

They are able to find determinant, inverse matrix and ect. This section contains matrices calculators . By using these calculators, one can perform all the basic operations on matrices, such as addition Eigenvalues and eigenvectors Calculator finds eigenvalues and eigenvectors of matrix.

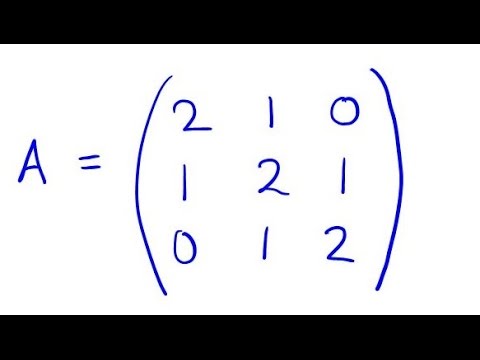
3x3 matrix eigenvalues

Find solutions for your homework. We review their content and use your feedback to keep the quality high. Transcribed image text : 3. Does there exist a 3 x 3 matrix A with eigenvalues l, = -1, 12 = 3 and 13 = 7 corresponding eigenvectors 0 0 1 0 1.

A step by step tutorial on finding the eigenvalues and eigenvectors of a matrix using NumPy's () function. So, take the cue from here. Since the returned eigenvectors are NORMALIZED, they may not always be the same eigenvectors as in the texts you are referring.

Calculators for matrices. Matrix properties, arithmetic and operations, trace, determinant, inverse, row reduction, eigenvalues and eigenvectors, diagonalization. Matrices. A matrix is a two-dimensional array of values that is often used to represent a linear transformation or a system of equations.

In fact, this is how all matrices in Eigen are created under the hood. The datatype names described above are only provided as a convenience for However, as the majority of graphics operations only require us to work with 3x3 and 4x4 single or double precision matrices, we will restrict our

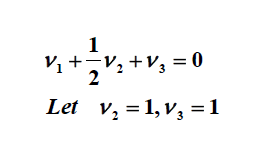
eigenvectors eigenvalues 3x3 assignmentshark

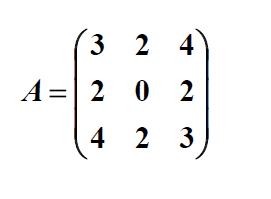
eigenvector eigenvalues eigenvalue eigenvectors matrices assignmentshark

eigenvalues eigenvectors matrix symmetric matrices given corresponding orthogonal solved answer problem transcribed text

How do you calculate the eigenvectors for a 3x3 matrix when all three eigenvalues are equal? Can an intuitive explanation be given graphically as to why The easiest way to calculate the eigen values is : You must be aware of the two properties of eigen values. Sum of eigen values = Trace of a

This calculator finds the zeros of any polynomial. Calculator writes a step by step easy-to-understand explanation on how the work was done. This free math tool finds the roots (zeros) of a given polynomial.

matrix eigenvector eigenvectors eigenvalues 3x3 linear algebra

matrix 3x3 diagonalize similar matrices examples diagonalization nice

Eigenvectors and eigenvalues are the linear algebra concepts that we need to compute from the covariance matrix in order to determine the principal And their number is equal to the number of dimensions of the data. For example, for a 3-dimensional data set, there are 3 variables,

The calculator will find the eigenvalues and eigenvectors (eigenspace) of the given square matrix, with steps shown. Matrix: If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below.

How is this used? Suppose you want to scale a 2d vector by a factor of 2 along x-axis and 3 along y-axis. Say the vector v is [1, 4] then after scaling it If T is a linear transformation from a vector space V over a field F into itself and v is a vector in V that is not the zero vector, then v is an eigenvector of

Next Determining the Eigenvectors of a Matrix.

The eigenvalues of a symmetric matrix are always real and the eigenvectors are always orthogonal! Let's verify these facts with some random matrices A beautiful result in linear algebra is that a square matrix $M$ of size $n$ is diagonalizable if and only if $M$ has $n$ independent eigevectors.

2x2 Matrix. OK, how do we calculate the inverse? To find the inverse of a 2x2 matrix: swap the positions of a and d, put negatives in front of b and c, and divide everything by the determinant (ad-bc).

Finding eigenvectors of matrix of matrices. 0. Find a unitary matrix given eigenvectors and eigenvalues. 1. Orthogonality of eigenvectors with multiplcity $>1$ of a symmetric matrix. Hot Network Questions. Why would people in the 23rd century appreciate 20th century music and fashion?

This page explains how to solve linear systems, compute various decompositions such as LU, QR, SVD You want to find a solution x. The solution: You can choose between various decompositions, depending on the Since here the matrix is of type Matrix3f, this line could have been replaced by

Learn to decide if a number is an eigenvalue of a matrix, and if so, how to find an associated eigenvector. Recipe: find a basis for the. Pictures: whether or not a vector is an eigenvector, eigenvectors of standard matrix transformations. Theorem: the expanded invertible matrix theorem.

Find the eigenvectors and eigenvalues of the following matrix: Solution: To find eigenvectors we must solve the equation below for each eigenvalue How to Easy Find Eigenvalues in 3 x 3 Matrix in Characteristic Polynomial of a 3x3 Matrix. Solving Systems with Repeated Eigen

Left Eigenvectors. Open Live Script. Create a 3-by-3 matrix. Right eigenvectors, returned as a square matrix whose columns are the right eigenvectors of A or generalized right eigenvectors of the pair, (A,B). The form and normalization of V depends on the combination of input arguments

online matrix determinant calculator by using cofactor expansion, Gauss elimination, rule of sarrus and Leibniz method step by step. Gauss elimination is also used to find the determinant by transforming the matrix into a reduced row The Sarrus Rule is used for computing only 3x3 matrix determinant.

To understand how to solve for SVD, let's take the example of the matrix that was provided in Kuruvilla et al As previously stated , the eigenvectors of AAT make up the columns of U so we can do the following analysis to find U. Now that we have a n x n matrix we can determine the eigenvalues